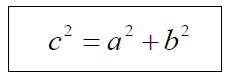ทฤษฎีบทปีทาโกรัส

ข้อควรรู้เกี่ยวกับ ทฤษฎีบทปีทาโกรัส

                    ปีทาโกรัสได้ศึกษาค้นคว้าเกี่ยวกับความสัมพันธ์ระหว่างด้านตรงข้ามมุมฉากและด้านประกอบมุมฉากของสามเหลี่ยมมุมฉาก ซึ่งเป็นทฤษฎีบทที่เก่าแก่และมีชื่อเสียงที่สุดบทหนึ่ง ได้แก่ทฤษฎีบทปีทาโกรัส ซึ่งมีใจความว่า ในสามเหลี่ยมมุมฉากใดๆ พื้นที่ของสี่เหลี่ยมจัตุรัสบนด้านตรงข้ามมุมฉาก จะเท่ากับผลบวกของพื้นที่สี่เหลี่ยมจัตุรัสบนด้านประกอบมุมฉาก

ตัวอย่าง 

                    จงเขียนความสัมพันธ์ระหว่างความยาวของด้านของรูปสามเหลี่ยมมุมฉากต่อไปนี้ ตามทฤษฎีบทของปีทาโกรัส

วิธีทำ 

พิจารณาความสัมพันธ์ระหว่างความยาวด้านของรูปสามเหลี่ยมมุมฉากตามทฤษฎีบทปีทาโกรัส

อัตราส่วนตรีโกณมิติ

                    ถ้าให้ ABC เป็นรูปสามเหลี่ยมมุมฉากที่มีมุมฉากที่ C และมี a , b , c เป็นความยาวของด้านตรงข้ามมุม A , B และ C ตามลำดับ

อัตราส่วนตรีโกณมิติ คือ อัตราส่วนที่เกิดจากความยาวของด้านของรูปสามเหลี่ยมมุมฉาก

เรียกอัตราส่วนทั้งสามนี้ว่า อัตราส่วนตรีโกณมิติของ A เมื่อ A เป็นมุมแหลมในรูปสามเหลี่ยม มุมฉากหรืออาจสรุปได้ว่า

ตัวอย่าง 

กำหนดรูปสามเหลี่ยมมุมฉาก ABCมีมุม C เป็นมุมฉาก มีความยาวด้านทั้งสาม ดังรูป จงหาค่าต่อไปนี้

1. sin A, cos A และ tan A
2. sin B, cos B และ tan B

วิธีทำ 

กำหนด ABC เป็นรูปสามเหลี่ยมมุมฉาก มีมุม C เป็นมุมฉาก จากทฤษฎีบทปีทาโกรัส จะได้ว่า

(1) หาค่า sin A, cos A และ tan A โดยการพิจารณาที่มุม A

(2) หาค่า sin B, cos B และ tan B โดยการพิจารณาที่มุม B

ข้อสังเกต 

ถ้า ABC เป็นรูปสามเหลี่ยมมุมฉากที่มีมุม C เป็นมุมฉากแล้วจะได้ว่า

สมบัติสามเหลี่ยมมุมฉาก

สมบัติสามเหลี่ยมมุมฉาก

                    ถ้าให้ ABC เป็นรูปสามเหลี่ยมมุมฉาก ที่มีมุมฉากที่ C และมี a , b , c เป็นความยาวของด้านตรงข้ามมุม A , B และ C ตามลำดับ

c แทนความยาวด้านตรงข้ามมุมฉาก
a และ b แทนความยาวของด้านประกอบมุมฉาก
จะได้ความสัมพันธ์ระหว่างความยาวของด้านทั้งสามของรูปสามเหลี่ยมมุมฉากดังต่อไปนี้

เมื่อ a แทนความยาวของด้านตรงข้ามมุม A
b แทนความยาวของด้านตรงข้ามมุม B
c แทนความยาวของด้านตรงข้ามมุม C

สมบัติสามเหลี่ยมคล้าย

สมบัติสามเหลี่ยมคล้าย

    พิจารณารูปสามเหลี่ยมสองรูปที่มีขนาดของมุมเท่ากัน 3 คู่ ดังนี้ถ้ารูปสามเหลี่ยม 2 รูป มีมุมเท่ากันมุมต่อมุมทั้ง 3 คู่ แล้ว สามเหลี่ยม 2 รูปนี้จะคล้ายกัน ดังรูป 

จากรูป 

 ดังนั้น รูปสามเหลี่ยม ABC คล้ายกับรูปสามเหลี่ยม XYZ และจากสมบัติการคล้ายกันของ รูปสามเหลี่ยมจะได้ผลตามมาคือ

เมื่อ a,b,c เป็นความยาวของด้าน AB, BC และ AC ตามลำดับในสามเหลี่ยม ABC

x,y,z เป็นความยาวของด้าน XY,YZ และ XZ ตามลำดับในสามเหลี่ยม XYZ

                    นั่นคือ ถ้ามีรูปสามเหลี่ยมสองรูปคล้ายกัน อัตราส่วนของความยาวของด้านสองด้านของรูปสามเหลี่ยมรูปหนึ่ง จะเท่ากับอัตราส่วนของความยาวของด้านสองด้านของรูปสามเหลี่ยมอีกรูปหนึ่ง โดยที่ด้านของรูปสามเหลี่ยมที่หาความยาวนั้นจะต้องเป็นด้านที่สมนัยกันอยู่ตรงข้ามกับมุมที่เท่ากันในทำนองเดียวกัน ถ้ารูปสามเหลี่ยมทั้งสองเป็นรูปสามเหลี่ยมมุมฉาก ซึ่งมีมุมที่ไม่เป็นมุมฉากเท่ากันสมมติว่าเป็นมุม A เท่ากับมุม X ดังรูป

พบว่า รูปสามเหลี่ยมสองรูปนี้คล้ายกัน ( มีมุมเท่ากันมุมต่อมุม ทั้ง 3 คู่ )

สรุป 

                    ไม่ว่ารูปสามเหลี่ยมดังกล่าวจะมีขนาดใหญ่หรือเล็กก็ตาม ถ้ารูปสามเหลี่ยม ทั้งสองรูปคล้ายกันแล้ว อัตราส่วนความยาวของด้านสองด้านของรูปสามเหลี่ยมรูปหนึ่งจะเท่ากับอัตราส่วนของความยาวของด้านสองด้านของรูปสามเหลี่ยมอีกรูปหนึ่งที่สมนัยกันเสมอ ( ด้านที่กล่าวถึงนี้ต้องเป็นด้านที่อยู่ตรงข้ามกับมุมที่เท่ากัน )